双线性插值是一种数字图像中实现缩放的方法，相较于近邻差值和平均差值有着更好地缩放效果。

原理

在图像进行缩放时，有着不同的缩放方法，最常见的一种是根据缩放大小比例，计算每一个像素位置所对应的原大小的像素大致位置，然后把相对应的未知的像素值套入缩放后的图片中。算法如下图所示：

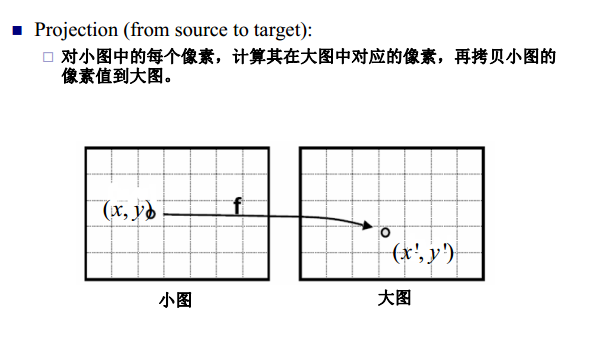
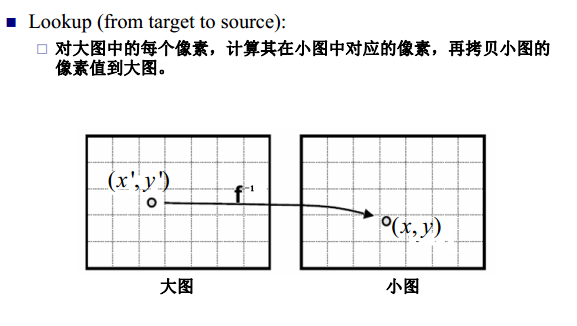
这种算法的不足之处在于，其在放大比例过大等情况下会导致明显失真。而双线性差值算法则有效地减少了这一问题，它根据距离上下左右的距离对不同的像素值（RGB 数值的大小）进行了加权相加，从而算出一个更接近的值代替。

算法

算法如下图：

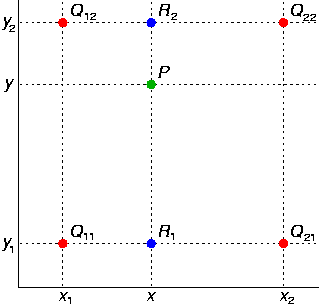
例子

下面是一个简单的运算例子。进行计算后，得出的放大后的图某像素对应的原图的位置 P 以及周围的四个像素点：

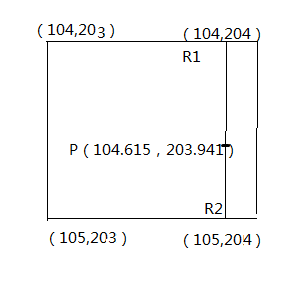
有 203.941 - 203 = 0.941

所以先对上面两个像素进行加权相加：

f(R1) = (1 - 0.941) * f(104, 203) + 0.941 * f(104,204)

同理对下面两个像素进行运算：

f(R2) = (1 - 0.941) * f(105, 203) + 0.941 * f(105, 204)

又有 104.615 - 104 = 0.615

所以上下算出来的值对应 y 轴再进行一次加权运算：

f(P) = (1 - 0.615) * f(R1) + 0.615 * f(R2)

最终所算出来的 f(P) 便是大图像素的值。

这个算法主要是通过加权来减轻由于均值或者直接代替所产生的误差，从而减小失真，在图像处理领域也十分常用。