最近花了些时间研究了一下图像相似度算法,感觉还是挺有趣的,也解决了我以前的一些疑惑。
目前的识别算法主要有几种,第一个是感知哈希算法,其中包括均值哈希(aHash)、感知哈希(pHash)和差异值哈希(dHash);第二种是 SIFT。而目前主要使用的是 SIFT 和 pHash。
下面简单介绍一下这几种算法的原理和优势。
均值哈希(aHash)
原理
- 缩放图片:将图片进行下采样至 8*8 的像素矩阵,共 64 个像素;
- 灰度图片:将图片转化为 256 阶的灰度图;
灰度算法有很多: 心理学灰度 $Gray=0.299\times R+0.587\times G+0.114\times B$ 平均值算法 $Gray=(R+G+B)/3$ 绿色值算法 $Gray=G$
- 二元化图片:将图片进行二元化转换;
这一步简单来说,就是先计算灰度均值,然后依次遍历原像素值,高于灰度值记为 1,低于记为 0,最后生成了一个 64 bits 的数列。
- 构造哈希:对 64 bits 的数列进行哈希,生成“感知指纹”;
- 对比指纹:对两幅图片的“指纹”计算汉明距离,距离越小则相似度越高。
算法特点
aHash 的算法简单粗暴,速度快。但是由于对图片进行了下采样和二值化,所以自然丢失了非常多的数据,精确度也就很低。
感知哈希(pHash)
原理
- 缩放图片:将图片进行下采样,生成正方形的图片(图片一般大于 8*8,3*32);
- 灰度图片:该步骤与上同;
- 计算 DCT(离散余弦变换):DCT 计算将图片按照频率分布进行分解;
- 裁剪 DCT:经过 DCT 操作后,会生成一个 32*32 的频域矩阵,我们只需要保存左上角的 8*8 即可,这一部分是图片的低频;
- 二元化矩阵:对上一步的矩阵进行处理,算法同样是计算平均值然后二元化;
- 构造哈希:对 64 bits 的数列进行哈希,生成“感知指纹”;
- 对比指纹:对两幅图片的“指纹”计算汉明距离,距离越小则相似度越高。
DCT 的算法相较复杂,主要用于数据或图像的压缩,能够将空域的信号转换到频域上,具有良好的去相关性的性能。 一维 DCT 变换: $$ F(u)=c(u)\sum_{i=0}^{N-1}f(i)cos[\frac{(i+0.5)\pi}{N}u] $$ $$ 在\space Y\neq f(x)\space时,L(Y,f(x))=1 $$ $$ 在\space Y=f(x)\space时,L(Y,f(x))=0 $$ 二维 DCT 变换: $$ F(u,v)=c(u)c(v)\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}f(i,j)cos[\frac{(i+0.5)\pi}{N}u]cos[\frac{(i+0.5)\pi}{N}v] $$ $$ 在\space u\neq 0\space时,c(u)=\sqrt{\frac{1}{N}} $$ $$ 在\space u=0\space时,c(u)=\sqrt{\frac{2}{N}} $$
算法特点
为了改善前辈 aHash 的精度,pHash 采用了 DCT(离散余弦变换),能够更好地压缩图片,并且保证一定的细节。这样的精度会高很多,但是因为要额外计算一次 DCT,所以速度也会慢一些。
差异值哈希(dHash)
原理
- 缩放图片:将图片进行下采样,生成 9*8 的图片,共 72 个像素点;
- 灰度图片:该步骤与上同;
- 计算差异:计算相邻像素之间的差异值,每行 9 个像素可以算出 8 个差异值,总共 8*8=64 个差异值;
- 二元化矩阵:比较差异值,若前一个大于后一个则为 1,小于等于则为 0;
- 构造哈希:对 64 bits 的数列进行哈希,生成“感知指纹”;
- 对比指纹:对两幅图片的“指纹”计算汉明距离,距离越小则相似度越高。
特点
这更像是一个性能和准确率折中的方案,运算速度比 pHash 快了很多(慢于 aHash),而精确度也比 aHash 更高(低于 pHash)。
SIFT 算法
上面介绍了感知哈希算法,三种方法大同小异,但都有一个缺点——鲁棒性不够高,以至于对图片进行了小幅度变换(调色、旋转等)就可能无法成功匹配,而这些问题 SIFT 算法就能够很好地解决。
SIFT 是尺度不变特征变换,这种算法具有尺度不变性,可在图中检测出关键点作为局部特征描述子。
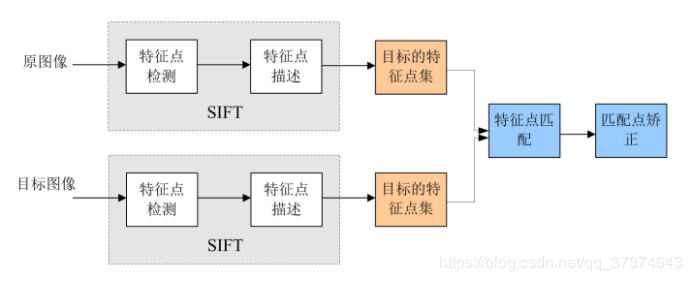
算法流程
- 提取特征点:提取一些十分突出的不会因光照、尺度、旋转等因素而消失的点,比如角点、边缘点、暗区域的亮点以及亮区域的暗点。
- 定位关键点并确定特征方向:在每个候选的点上,通过一个拟合精细的模型来确定位置和尺度。
- 通过各关键点的特征向量:对特征进行两两比较找出相互匹配的若干对特征点,建立对应关系。
算法特点
- 具有较好的稳定性和不变性,能够适应旋转、缩放、亮度的变化,具有较好的鲁棒性;
- 区分性好,能够胸海量数据中进行区分和匹配;
- 多量性,单个物体也能够产生大量特征向量;
- 高速性,能够快速进行特征向量匹配;
- 可扩展性,能够与其他的特征向量进行联合计算。
- 可扩展性,能够与其他的特征向量进行联合计算。