第一题:Shuffle String
给你一个字符串 s 和一个长度相同的整数数组 indices。请你重新排列字符串 s ,其中第 i 个字符需要移动到 indices[i] 指示的位置,返回重新排列后的字符串。
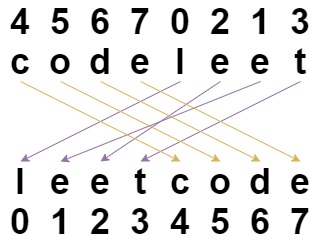
输入:s = "codeleet", indices = [4,5,6,7,0,2,1,3]
输出:"leetcode"
解释:如图所示,"codeleet" 重新排列后变为 "leetcode" 。
分析
这道题的算法比较简单,有两种解法。
第一种是在不能新建字符串空间的情况下,可以通过从开头遍历,然后根据 indices 循环交换字符串,直到 indices 正好为该位置的指针时,转到下一个继续进行循环交换。
第二种是可以新建字符串空间的情况,这样子就比较简单了,直接新建或复制出一个同等长度的字符串,然后根据 indices 遍历原字符串,然后放到新数组的对应位置即可。
很明显,第一种的时间复杂度为 $O(n^2)$,第二种的时间复杂度为 $O(n)$,所以最终提交的为第二种方法的代码。源码如下:
class Solution:
def restoreString(self, s: str, indices: List[int]) -> str:
m = [0] * len(indices) # 新建一个列表
for i,n in enumerate(indices):
m[n] = s[i] # 按照 indices 为指针,把字符放到新列表中的对应的位置
return "".join(m) # 用 join 把列表合成字符串
因为 Python 语言本身不支持字符串的枚举,所以只能生成列表进行操作,最后再合起来。而 C++ 可以直接枚举操作字符串,所以代码相对简单一些:
class Solution {
public:
string restoreString(string s, vector<int>& indices) {
string t = s; // 复制一个字符串
for(int i = 0; i < (int)s.size(); i++) {
t[indices[i]] = s[i]; // 按照 indices 为指针把字符放到新字符串对应的位置
}
return t;
}
};
第二题:Bulb Switcher IV
房间中有 n 个灯泡,编号从 0 到 n-1,自左向右排成一行。最开始的时候,所有的灯泡都是关着的。
请你设法使得灯泡的开关状态和 target 描述的状态一致,其中 target[i] 等于 1 第 i 个灯泡是开着的,等于 0 意味着第 i 个灯是关着的。
有一个开关可以用于翻转灯泡的状态,翻转操作定义如下:
选择当前配置下的任意一个灯泡(下标为 i)
翻转下标从 i 到 n-1 的每个灯泡
翻转时,如果灯泡的状态为 0 就变为 1,为 1 就变为 0 。
返回达成 target 描述的状态所需的最少翻转次数。
输入:target = "10111"
输出:3
解释:初始配置 "00000".
从第 3 个灯泡(下标为 2)开始翻转 "00000" -> "00111"
从第 1 个灯泡(下标为 0)开始翻转 "00111" -> "11000"
从第 2 个灯泡(下标为 1)开始翻转 "11000" -> "10111"
至少需要翻转 3 次才能达成 target 描述的状态
分析
这道题其实可以直接通过找规律解出。通过几个例子可以发现,其实反转的次数与所给的字符串中的 01 跳变次数的变化一致——当每一个字符串前面不上一个 '0' 的时候,跳变次数就等于反转次数。
Python 代码:
class Solution:
def minFlips(self, target: str) -> int:
temp = '0' # 一开始填个 0
final = 0 # 翻转次数
for n in target:
if n != temp:
final += 1 # 不等时 +1
temp = n # 替换 temp 值
return final
C++ 的写法:
class Solution {
public:
int minFlips(string target) {
int cur = 0, ans = 0;
for(char c : target) {
int d = c - '0';
if((d ^ cur) == 1) {
cur ^= 1;
ans++;
}
}
return ans;
}
};
二者在算法上是一致的。
第三题:Number of Good Leaf Nodes Pairs
给你二叉树的根节点 root 和一个整数 distance 。
如果二叉树中两个叶节点之间的 最短路径长度小于或者等于 distance,那它们就可以构成一组好叶子节点对。
返回树中好叶子节点对的数量。
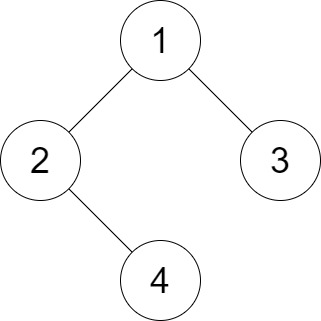
输入:root = [1,2,3,null,4], distance = 3
输出:1
解释:树的叶节点是 3 和 4 ,它们之间的最短路径的长度是 3 。这是唯一的好叶子节点对。
分析
这道题比前面两题要难一些,需要用到 DFS 算法去遍历 root 树,从而找出所有的小于 distance 的路径。
这道题的算法具体就是,从树的底层往上遍历,先对每一个节点计算到父节点的距离(因为子节点有多个,所以到父节点那儿是一组距离向量);然后父节点再根据子节点的距离参数计算自己到父节点的一组距离向量,以此类推。最后把小于 distance 的挑出来计数即可。
Python 代码如下:
class Solution:
def countPairs(self, root: TreeNode, d: int) -> int:
if not root:
return 0 # 常规判断空值
def dfs(root):
nonlocal ans # 使用非 local 的变量
if not (root.left or root.right):
return [1] # 如果没有子节点,就返回 [1]
l = dfs(root.left) if root.left else []
r = dfs(root.right) if root.right else []
for i, c1 in enumerate(l, start=1):
for c2 in r[:min(d - i, len(r))]:
ans += c1 * c2 # 计算满足条件的路径条数
cur = [0] * (max(len(l), len(r))+1) # 新建一个数组
for i in range(len(l)):
cur[i + 1] += l[i] # i + 1 处加上左树 i 的值,i + 1 是因为这个数组对应的每一位是层之间的距离
# 即第几层到本层的距离多少,然后加在一起(左右不分,全加一起)
for i in range(len(r)):
cur[i + 1] += r[i] # i + 1 处加上右树 i 的值
return cur[:min(d-1, len(cur))] # 只返回小于 distance 的数组(大于的后面计算就无意义了)
# 这样可以减少判断运算
ans = 0
dfs(root)
return ans
C++ 的代码如下:
class Solution {
public:
vector<int> dfs(TreeNode* t, int dis, int& ans) {
if (!t->left && !t->right) return {1};
vector<int> vl, vr, vt;
if (t->left) vl = dfs(t->left, dis, ans);
if (t->right) vr = dfs(t->right, dis, ans);
for (auto l : vl) for (auto r : vr) if (l + r <= dis) ++ans; // 遍历向量,计算满足条件的数量
for (auto l : vl) vt.push_back(l + 1); // 把左距离 + 1,然后添加到末尾
for (auto r : vr) vt.push_back(r + 1); // 同上
return vt;
}
int countPairs(TreeNode* root, int distance) {
int ans = 0;
dfs(root, distance, ans);
return ans;
}
};
C++ 的算法就比较简单粗暴,原理大致相同,就是往上加,然后满足条件的就使 ans++。此代码没有向 Python 一样剪枝,每次都去掉不满足条件的向量,这在部分情况下会增加运算量,还有一定的优化空间。
第四题:String Compression II
行程长度编码是一种常用的字符串压缩方法,它将连续的相同字符(重复 2 次或更多次)替换为字符和表示字符计数的数字(行程长度)。例如,用此方法压缩字符串 "aabccc" ,将 "aa" 替换为 "a2" ,"ccc" 替换为 "c3" 。因此压缩后的字符串变为 "a2bc3" 。
注意,本问题中,压缩时没有在单个字符后附加计数 '1' 。
给你一个字符串 s 和一个整数 k 。你需要从字符串 s 中删除最多 k 个字符,以使 s 的行程长度编码长度最小。
请你返回删除最多 k 个字符后,s 行程长度编码的最小长度。
输入:s = "aaabcccd", k = 2
输出:4
解释:在不删除任何内容的情况下,压缩后的字符串是 "a3bc3d" ,长度为 6 。最优的方案是删除 'b' 和 'd',这样一来,压缩后的字符串为 "a3c3" ,长度是 4 。
分析
在这道题的时候,我很快就想出了算法:统计词频,然后从小到大排列,再按顺序减就完了。
但是这道题并不是我想的那么简单,主要问题就出在最优减的解上面,我这个方法在小部分的题目中无法找出最优解(即最短字符串)。
比如说,有 9 个 a 和 10 个 b 的时候要减去 2 个,那么减 b 的数量才是最优解。如果实在上面的算法上加以改进的话,时间复杂度会飙升,所以最后还是选择了放弃(逃)
看到很多人没做出来,我也是平衡了很多。
大佬的 Python 代码如下:
from functools import lru_cache
from itertools import groupby
class Solution:
def getLengthOfOptimalCompression(self, S, K):
def rle(x):
if x <= 1: return x
return len(str(x)) + 1
N = len(S)
if N == K:
return 0
INF = int(1e9)
@lru_cache(None)
def dp(i, curlength, lastcur, eaten):
if eaten > K:
return INF
if i == N:
return 0
# Eat this character:
ans = dp(i + 1, curlength, lastcur, eaten + 1)
# Or add:
if S[i] == lastcur:
delta = rle(curlength + 1) - rle(curlength)
cand = dp(i + 1, curlength + 1, lastcur, eaten) + delta
if cand < ans: ans = cand
else:
cand = dp(i + 1, 1, S[i], eaten) + 1
if cand < ans: ans = cand
return ans
return dp(0, 0, '', 0)