第一题:Count Good Triplets
给你一个整数数组 arr ,以及 a、b、c 三个整数。请你统计其中好三元组的数量。
如果三元组 (arr[i], arr[j], arr[k]) 满足下列全部条件,则认为它是一个 好三元组 。
0 <= i < j < k < arr.length|arr[i] - arr[j]| <= a|arr[j] - arr[k]| <= b|arr[i] - arr[k]| <= c
其中 |x| 表示 x 的绝对值。
返回好三元组的数量。
示例:
输入:arr = [3,0,1,1,9,7], a = 7, b = 2, c = 3
输出:4
解释:一共有 4 个好三元组:[(3,0,1), (3,0,1), (3,1,1), (0,1,1)] 。
分析
这一道题可以直接穷举,然后遍历出所有符合的条件即可。但是直接穷举的话还是比较慢,需要剪枝提高效率。剪枝的方法是先判断第一个条件,满足之后再进行下面的循环,这样可以在测试集中减少接近一半的时间。
代码
Python
class Solution:
def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:
length = len(arr)
token = 0
for i in range(length - 2): # 第一个数
for j in range(i + 1, length - 1): # 第二个数
if abs(arr[i] - arr[j]) <= a: # 在满足第一个条件之后再取第三个数
for k in range(j + 1, length): # 第三个数
if (abs(arr[j] - arr[k]) <= b and abs(arr[i] - arr[k]) <= c): # 继续判断后两个条件
token += 1 # 满足则 +1
return token
C++
class Solution {
public:
int countGoodTriplets(vector<int>& arr, int a, int b, int c) {
int length = arr.size();
int token = 0;
for(int i = 0; i <= length - 3; ++i){
for(int j = i + 1; j <= length - 2; ++j){
if(abs(arr[i] - arr[j]) <= a){ // 判断完第一个条件再取第三个数
for(int k = j + 1; k < length; ++k){
if(abs(arr[j] - arr[k]) <= b && abs(arr[i] - arr[k]) <= c)
token++;
}
}
}
}
return token;
}
}
第二题:Find the Winner of an Array Game
给你一个由不同整数组成的整数数组 arr 和一个整数 k 。
每回合游戏都在数组的前两个元素(即 arr[0] 和 arr[1] )之间进行。比较 arr[0] 与 arr[1] 的大小,较大的整数将会取得这一回合的胜利并保留在位置 0 ,较小的整数移至数组的末尾。当一个整数赢得 k 个连续回合时,游戏结束,该整数就是比赛的赢家。
返回赢得比赛的整数。
题目数据保证游戏存在赢家。
示例:
输入:arr = [2,1,3,5,4,6,7], k = 2
输出:5
解释:一起看一下本场游戏每回合的情况:
Round | arr | winner | win_count
1 | [2,1,3,5,4,6,7] | 2 | 1
2 | [2,3,5,4,6,7,1] | 3 | 1
3 | [3,5,4,6,7,1,2] | 5 | 1
4 | [5,4,6,7,1,2,3] | 5 | 2
因此将进行 4 回合比赛,其中 5 是赢家,因为它连胜 2 回合。
分析
这道题的话其实就相当于是多了个中断条件的比较算法,当连胜(也就是连续大于)一定次数,或者该数已成为数列最大值的时候就直接返回,因为当是最大值的时候,再接着比下去是没有意义的。
因为我求快心切,用了 Python 和最直观的算法,最开始的 Python 代码如下:
class Solution:
def getWinner(self, arr: List[int], k: int) -> int:
token = 0
while token < k:
if arr[0] > arr[1]: # 赢了
token += 1
arr = [arr[0]] + arr[2:] + [arr[1]] # 把第二个给移到后面
else:
token = 1 # 输了置一
arr = arr[1:] + [arr[0]] # 把第一个移到后面
return arr[0]
结果发现超时了(笑),因为测试集有一个 100000000 次的,所以用这个最原始直观的方法会直接硬着头皮循环 100000000 次,但实际上后面的循环是没有意义的,十分耗时。所以后来就优化,改成了最终版本。
代码
Python
class Solution:
def getWinner(self, arr: List[int], k: int) -> int:
token = 0
index = 0
while token < k and index < len(arr) - 1: # k 次数达到了,或者 index 到了最后时停止
if arr[index] > arr[index + 1]:
arr[index + 1] = arr[index] # 交换值
token += 1 # 加一
else:
token = 1 # 小于就不加一
index += 1 # 每轮比较 index 自增一
return arr[index] # 返回当前的值
C++
class Solution {
public:
int getWinner(vector<int>& arr, int k) {
int i = 0, t = 0; // 算法与 Python 的基本一致
while(t < k && i < arr.size() - 1){
if(arr[i] > arr[i+1]){
arr[i+1] = arr[i]; // 赢了就交换值,token 加一
++t;
}else
t = 1;
++i; // 每轮 index 自增一
}
return arr[i]; // 返回当前的值
}
};
第三题:Minimum Swaps to Arrange a Binary Grid
给你一个 n x n 的二进制网格 grid,每一次操作中,你可以选择网格的相邻两行进行交换。
一个符合要求的网格需要满足主对角线以上的格子全部都是 0 。
请你返回使网格满足要求的最少操作次数,如果无法使网格符合要求,请你返回 -1 。
主对角线指的是从 (1, 1) 到 (n, n) 的这些格子。
示例:

输入:grid = [[0,0,1],[1,1,0],[1,0,0]]
输出:3
分析
这道题虽然明面上是一道线性代数的三角矩阵化简问题,实际上却不是。如果将每一行从右到左的连续 0 的数量值生成出来形成一个新的数组,就会发现这其实是一道计算冒泡排序的步数的问题。
比如例子中的 grid 可以化简为一个 0 的数量的列表 [0, 1, 2],然后由这个列表变为 [2, 1, 0] 的步骤数就是最终的结果了。这么想的话这一道题的解法就会方便很多。我一开始写的一个算法虽然十分简洁快速,但是只能满足完全对角的矩阵判断。所以还是参考了大佬的算法自己再按着之前的算法改进了一下,提交了最后的 AC 版本。
代码
Python
class Solution:
def minSwaps(self, grid: List[List[int]]) -> int:
if not grid:
return 0
n = len(grid)
nums = [] # 该列表存放每行从右到左的 0 个数
for i in range(n):
j = n - 1
while j >= 0 and grid[i][j] == 0:
j -= 1
nums.append(n - 1 - j)
steps = 0
for i in range(n - 1):
need_zeros = n - 1 - i
j = i
while j < len(nums) and nums[j] < need_zeros:
j += 1 # 不满足要求则 j + 1,继续判断下一行,满足或者到边界则跳出
if j == len(nums): # 等于数组长度则证明没有满足的行,返回 -1
return -1
steps += j - i # 满足则加上步数
nums.insert(i, nums.pop(j)) # 换序,把该位置的值插到前面对应的 i 位置处
return steps
太晚了,就没有写 C++ 的版本,网上随便找了一份,简单看了一下,算法是一模一样的,都是判断然后计数:
C++
class Solution {
public:
int minSwaps(vector<vector<int>>& grid) {
int n = grid.size(); //网格规模
vector<int> a; //记录每一行后缀0个数的数组
for(int i = 0; i < n; i++)
{
int count = 0;
for(int j = n - 1; j >= 0; j--)
{
if(grid[i][j] == 0) count++; //数每一行的后缀0
else break;
}
a.push_back(count);
}
int count = 0; //交换次数
for(int i = 0; i < n - 1; i++)
{
if(a[i] >= n - i - 1) continue;//满足条件,该行直接跳过
else{//不满足条件
int j = i; //用新参数遍历找满足条件的后缀0
for(; j < n; j++)
{
if(a[j] >= n - i - 1) break;
}
if(j == n) return -1; //找不到,直接返回-1
for(; j > i; j--) //找到了最先满足条件的后缀0个数
{
swap(a[j], a[j - 1]); //每一行交换上去
count++; //记录交换次数
}
}
}
return count;
}
};
第四题:Get the Maximum Score
你有两个有序且数组内元素互不相同的数组 nums1 和 nums2 。
一条合法路径定义如下:
选择数组 nums1 或者 nums2 开始遍历(从下标 0 处开始)。从左到右遍历当前数组。如果你遇到了 nums1 和 nums2 中都存在的值,那么你可以切换路径到另一个数组对应数字处继续遍历(但在合法路径中重复数字只会被统计一次)。得分定义为合法路径中不同数字的和。请你返回所有可能合法路径中的最大得分。
由于答案可能很大,请你将它对 10^9 + 7 取余后返回。
示例:
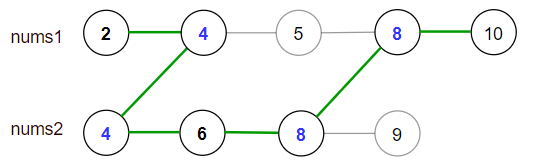
输入:nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]
输出:30
解释:合法路径包括:
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10],(从 nums1 开始遍历)
[4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] (从 nums2 开始遍历)
最大得分为上图中的绿色路径 [2,4,6,8,10] 。
分析
这道题有点出乎我的意料,比第三题要简单一些。说白了就是找到两条路中路径最大的一条,其中两条路的值相同的节点之间可以相互切换,所以这就有两个算法:
-
第一种是双指针法,因为两个都是有序数列,所以每轮哪个小就推哪个,然后分别记录值,到相同的节点时把两者中较大的一个路径值加入总路径值中。
-
第二种是哈希 + sum 算法,先把
nums1序列生成字典,然后第二个数组nums2每一个值比配时,都会都检索一遍nums1的哈希,然后取出对应值的指针。这里快的原因是字典在索引的时候是用的哈希算法,比普通的便利要快上很多。
第二种算法本质上和第一个差不多,但是由于哈希 + sum 比遍历快,所以整体速度也快一些。第一个算法比较简单,所以我就直接用了第二种方法提交了 AC 版本。
代码
Python
class Solution:
def maxSum(self, nums1: List[int], nums2: List[int]) -> int:
d = {t: i for i, t in enumerate(nums1)} # 转成字典
ans = 0
p, q = 0, 0
for j, t in enumerate(nums2):
if t in d:
i = d[t] # 哈希算法,取出指针
ans += max(sum(nums1[p: i]), sum(nums2[q: j])) # 当前相同值的指针到上一对相同指针之间的值求和的最大值
p, q = i, j # 更新指针
ans += max(sum(nums1[p: ]), sum(nums2[q: ]))
return ans % 1000000007 # 按要求,最后返回余数
C++ 的代码就是算法一的双指针版本。
C++
int maxSum(vector<int>& nums1, vector<int>& nums2) {
long sum1 = 0, sum2 = 0;
long res = 0;
int i = 0, j = 0;
while(i < nums1.size() && j < nums2.size()){
if(nums1[i] == nums2[j]){
res += (max(sum1, sum2) + nums1[i]);
sum1 = 0;
sum2 = 0;
i++;
j++;
}
else if(nums1[i] < nums2[j]){
sum1 += nums1[i];
i++;
}
else{
sum2 += nums2[j];
j++;
}
}
while(i < nums1.size()){
sum1 += nums1[i];
i++;
}
while(j < nums2.size()){
sum2 += nums2[j];
j++;
}
res += max(sum1, sum2);
return res % ((int)pow(10, 9) + 7 );