LeetCode Weekly Contest 201 Review.

第一题：Make The String Great

给你一个由大小写英文字母组成的字符串 s 。

一个整理好的字符串中，两个相邻字符 s[i] 和 s[i + 1] 不会同时满足下述条件：

  • 0 <= i <= s.length - 2
  • s[i] 是小写字符，但 s[i + 1] 是相同的大写字符；反之亦然。

请你将字符串整理好，每次你都可以从字符串中选出满足上述条件的两个相邻字符并删除，直到字符串整理好为止。

请返回整理好的字符串。题目保证在给出的约束条件下，测试样例对应的答案是唯一的。

注意：空字符串也属于整理好的字符串，尽管其中没有任何字符。

示例：

输入：s = "leEeetcode"
输出："leetcode"
解释：无论你第一次选的是 i = 1 还是 i = 2，都会使 "leEeetcode" 缩减为 "leetcode" 。

分析

这一题的意思就是说，遍历整个字符串，然后如果当前的字符和下一个字符大小写不同，字母相同的时候，则删除两个字母，直到整个字符串满足条件为止。

所以就遍历然后写一个判断条件判断即可。可以通过每次匹配到之后遍历指针归零的方式，来减少每一次的遍历长度；同时，考虑到归零也有可能出现无意义的匹配，所以可以在匹配到字符串之后指针减一（即从上一个字符继续匹配），这样就可以进一步减少无意义的匹配。

这样的题需要用到自己构建的指针遍历，所以要注意 out of range 的问题。

代码

Python

class Solution:
    def makeGood(self, s: str) -> str:

        if not s: return ""  # 非空继续

        i = 0  # 初始化指针

        while i <= len(s) - 2:  # 指针范围
            if s[i] == s[i + 1]:  # 如果相等就下一个
                i += 1
            elif abs(ord(s[i]) - ord(s[i + 1])) == 32:  # 不相等则判断是否满足条件
                s = s[:i] + s[i + 2:]  # 删除两个字符
                i = max(0, i - 1)  # i -= 1
            else:
                i += 1

        return s

C++

class Solution {
public:
    string makeGood(string s) {
        int i = 0;
        while (i < s.size()) {
            if (i + 1 == s.size()) break;
            if (abs(s[i] - s[i + 1]) == 32) {
                s.erase(i, 2);
                i = max(0, i - 1);
            } else {
                i += 1;
            }
        }
        return s;
    }
};

C++ 的算法和 Python 的一致，所以就不做注释了。

第二题：Find Kth Bit in Nth Binary String

给你两个正整数 n 和 k，二进制字符串  Sn 的形成规则如下：

  • S1 = "0"
  • 当 i > 1 时，Si = Si-1 + "1" + reverse(invert(Si-1))

其中 + 表示串联操作，reverse(x) 返回反转 x 后得到的字符串，而 invert(x) 则会翻转 x 中的每一位（0 变为 1，而 1 变为 0）

例如，符合上述描述的序列的前 4 个字符串依次是：

  • S1 = “0”
  • S2 = “011”
  • S3 = “0111001”
  • S4 = “011100110110001”

请你返回 Sn 的 第 k 位字符，题目数据保证 k 一定在 Sn 长度范围以内。

示例：

输入：n = 3, k = 1
输出："0"
解释：S3 为 "0111001"，其第 1 位为 "0" 。

分析

第二题就是跟着题目的要求来算就可以解决了，就是总共进行 k 次运算，然后每一次运算就是 s = s + '1' + reverse(invert(s))，invert 是指把每一个 0 和 1 取反，最后输出第 k - 1 个数字，格式为 str。

这里要注意，只进行 n - 1 次运算（第一次已给出），然后输出的字符是第 k - 1 个字符。

算法并不难，主要是复杂度的优化，即如何更快地提高速度。我一开始直接使用的方法是通过了一个简单快速的方式（如下面 Python 1 解法）生成出一个数字序列（这样方便运算，并且比字符串更快），然后再输出第 k - 1 个数字的字符格式即可。

这个解法拿到了 100% 和 75%，我还是很满意的。但是后来看到了黄歪歪大佬的代码（Python 2 和 C++ 解法），他的算法更加有效率，直接使用了 ^= 运算去求，并且没有生成 s 字符串产生额外的空间消耗。

还有一种 DP 的解法，也贴在了下面（Python 3 解法）。

代码

Python 1

class Solution(object):
    def findKthBit(self, n, k):
        s = [0]
        tmp = [1, 0]  # 这个是为了方便取反
        for i in range(n - 1):  # 进行 n - 1 次运算
            s += [1] + [tmp[n] for n in s[::-1]]  # 这样写生成代码就优雅很多

        return str(s[k - 1])  # 输出 str 类型

Python 2

def findKthBit(self, n, k):
    flip = 0
    l = 2 ** n - 1
    while k > 1:
        if k == l / 2 + 1:
            return str(1 ^ flip)
        if k > l / 2:
            k = l + 1 - k
            flip = 1 - flip
        l /= 2
    return str(flip)

Python 3

class Solution:
    def findKthBit(self, n: int, k: int) -> str:

        length = [0]*21
        length[1] = 1
        for i in range(2, 21):
            length[i] = length[i-1] *2 + 1

        def dp(n, k):
            if n == 1 and k == 1:
                return 0

            total = length[n]
            if k == total // 2 + 1:
                return 1

            if k < total // 2 + 1:
                return dp(n-1, k)
            else:
                return 1 - dp(n-1, (total//2+1)*2 - k)

        ans = dp(n, k)
        return '1' if ans == 1 else '0'

C++

char findKthBit(int n, int k) {
    int flip = 0, l = (1 << n) - 1;
    while (k > 1) {
        if (k == l / 2 + 1)
            return '0' + (flip ^ 1);
        if (k > l / 2) {
            k = l + 1 - k;
            flip ^= 1;
        }
        l /= 2;
    }
    return '0' + flip;
}

第三题：Maximum Number of Non-Overlapping Subarrays With Sum Equals Target

给你一个数组 nums 和一个整数 target。

请你返回非空不重叠子数组的最大数目，且每个子数组中数字和都为 target。

示例：

输入：nums = [1,1,1,1,1], target = 2
输出：2
解释：总共有 2 个不重叠子数组（加粗数字表示） [1,1,1,1,1] ，它们的和为目标值 2 。

分析

有一说一，这一题一开始我直接给想复杂了，想着去用 DFS 把所有满足的列表给遍历出来，然后再加上一个去重的算法去掉重复的，最后得出结果。但是到了去重给我难住了，因为我考虑到了很多种交集的可能，但就是不知道怎么去掉重复的（比如列表中有重复值的情况）。

后来看了大家伙的代码，我就发现原来这道题没必要想得那么复杂，题目中的要求是一个连续的子列表，也就是不存在中间跳过一个的情况，自然也就不用 DFS 去遍历了。所以这道题就可以简化成一个求积分区间和等于 target 值的列表数量的题，方法就是直接遍历整个列表，然后往上求每一个点到开头的积分和，有一个表存储每一个点从列表开头的值的各个求和数，然后每一次都匹配这个表是否有满足的；如果不满足 sum == target 的话就存入表中，若满足就 res += 1，然后其他的变量归零，即从下个点重新计算积分和。

这一块的解法分析可能比较意识流，talk is cheap and see the code，代码可能会更直观一些。

代码

Python

class Solution(object):
    def maxNonOverlapping(self, nums, target):
        s, sums, ans= {0}, 0, 0  # 初始化
        for num in nums:
            sums += num  # 求和加上当前值
            if sums - target in s:  # 这里就是判断是否前面有一个点到此点的求和值为 target
                ans += 1  # 有则 ans + 1
                s,sums = {0}, 0  # 归零
            else:
                s.add(sums)  # 没有就加进去，供后面的遍历
        return ans

C++

class Solution {
public:
    int maxNonOverlapping(vector<int> &nums, int target) {
        unordered_map<int, int> mp;
        mp[0] = -1;
        int sum = 0, end = -1;
        int ret = 0;
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];
            if (mp.find(sum - target) != mp.end()) {
                if (mp[sum - target] + 1 > end) {
                    ret++;
                    end = i;
                }
            }
            mp[sum] = i;
        }
        return ret;
    }
};

C++ 的代码使用了哈希表。

第四题：Minimum Cost to Cut a Stick

有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的最小总成本。

示例：

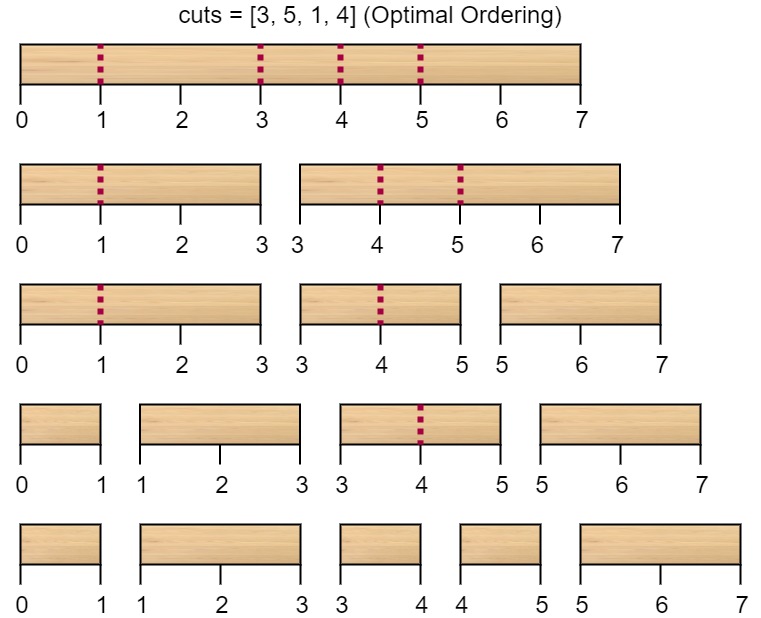
输入：n = 7, cuts = [1,3,4,5]
输出：16
解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：


第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

分析

这题给我看蒙了，因为我本身 DP 不是特别熟练，所以这道题我优先想着使用特殊的方法去解，比如每次都取中间的值（这是错的），结果就没做出来。

然后看了看其他人的代码，他们都是用的 DP 来求解。就是通过遍历所有的可能，然后每一步求出一个最小值，得出最后的一个最小值。看大佬们的说法，在比赛的时候如果使用 lru_cache 的话（Python 1 解法）写代码的速度会快很多，但是时间可能就没有建立矩阵的 DP （Python 2 解法）来的快速。

代码

Python 1

class Solution4:
    def minCost(self, n: int, cuts: List[int]):
        cuts=[0]+cuts+[n]
        cuts.sort()

        @functools.lru_cache(None)
        def dp(l, r):
            if  l >= r - 1:
                return 0
            ans = math.inf
            for k in range(l + 1,r):
                new_v = dp(l, k) + dp(k, r) + cuts[r] - cuts[l]  # r - l 就是当前棍子的长度
                ans = min(ans, new_v)
            return ans if ans != math.inf else 0

        return dp(0, len(cuts)-1)

Python 2

    def minCost(self, n, A):
        A = sorted(A + [0, n])
        k = len(A)
        dp = [[0] * k for _ in range(k)]
        for d in range(2, k):
            for i in range(k - d):
                dp[i][i + d] = min(dp[i][m] + dp[m][i + d] for m in range(i + 1, i + d)) + A[i + d] - A[i]
        return dp[0][k - 1]

这个从整体上来说算法是和上面的一样的，但是结构上精简优化了很多。

C++

class Solution {
public:
    // 为了方便实现，
    // dp[l][r] 代表 切割以 cuts[l], cuts[r] 为左右端点的木棍的最小花费
    int dp[103][103];
    int dfs(int l, int r, const vector<int>& cuts) {
        // 保存已经计算过的答案，避免子问题的重复计算
        if(dp[l][r] != -1) {
            return dp[l][r];
        }
        // l+1 == r 时，说明不用再切了。
        if(l+1 == r) {
            dp[l][r] = 0;
            return 0;
        }
        // 枚举切割的地方，记录最优解。
        for(int i = l+1; i < r; i++) {
            int cost = dfs(l, i, cuts) + dfs(i, r, cuts) + cuts[r] - cuts[l];;
            if(dp[l][r] == -1 || dp[l][r] > cost) {
                dp[l][r] = cost;
            }
        }
        return dp[l][r];
    }
    
    int minCost(int n, vector<int>& cuts) {
        memset(dp, -1, sizeof(dp));
        cuts.push_back(0);
        cuts.push_back(n);
        sort(cuts.begin(), cuts.end());
        // 向 cuts 中加入 0 和 n。
        // 这不会影响答案，因为我们不会从这两处切割。
        return dfs(0, cuts.size()-1, cuts);
    }
};

C++ 的代码是直接从网上摘的，也是用了 DP 的算法。

Copyright © 2023 CC-BY-NC-4.0 LICENSE All Rights Reserved. Built by Zee with ❤.