每一道题目都附上了链接,现在可以更直接地进入题目了。
第一题:圆形赛道上经过次数最多的扇区
给你一个整数 n 和一个整数数组 rounds 。有一条圆形赛道由 n 个扇区组成,扇区编号从 1 到 n 。现将在这条赛道上举办一场马拉松比赛,该马拉松全程由 m 个阶段组成。其中,第 i 个阶段将会从扇区 rounds[i - 1] 开始,到扇区 rounds[i] 结束。举例来说,第 1 阶段从 rounds[0] 开始,到 rounds[1] 结束。
请你以数组形式返回经过次数最多的那几个扇区,按扇区编号升序排列。
注意,赛道按扇区编号升序逆时针形成一个圆(请参见第一个示例)。
示例:
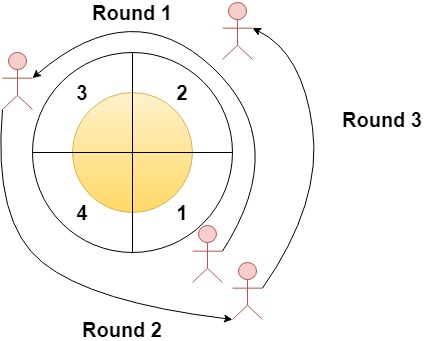
输入:n = 4, rounds = [1,3,1,2]
输出:[1,2]
解释:本场马拉松比赛从扇区 1 开始。经过各个扇区的次序如下所示:
1 --> 2 --> 3(阶段 1 结束)--> 4 --> 1(阶段 2 结束)--> 2(阶段 3 结束,即本场马拉松结束)
其中,扇区 1 和 2 都经过了两次,它们是经过次数最多的两个扇区。扇区 3 和 4 都只经过了一次。
分析
这道题的意思就是统计所有经过的块,然后输出经过次数最多块的列表。但其实这道题还可以进行化简,因为每转一圈,圈上的每一块都加一,这跟不加是一样的(因为所有的都一起加了),所以之用考虑开头和结尾经过的块即可。
代码
Python
class Solution:
def mostVisited(self, n: int, rounds: List[int]) -> List[int]:
tmp_l = rounds[0] # 最左边的数字
tmp_r = rounds[-1] # 最右边的数字
if tmp_l == tmp_r:
return [tmp_r] # 相等则返回该数字
elif tmp_r < tmp_l: # 如果两边数字不相等,则可化简为从左数字到右数字的一轮
return [n for n in range(1, tmp_r + 1)] + [m for m in range(tmp_l, n + 1)]
# 如果右边的数字比左边的小,即 [左到最大] + [1 到最右] 的数列
else:
return [n for n in range(tmp_l, tmp_r + 1)]
# 反之就是 [左到右] 的数列
C++
class Solution {
public List<Integer> mostVisited(int n, int[] rounds) {
int start = rounds[0];
int end = rounds[rounds.length - 1];
if (start == end) return Arrays.asList(start);
List<Integer> result = new ArrayList<>();
if (start < end) {
for (int i = start; i <= end; i++) {
result.add(i);
}
return result;
}
//start>end
for (int i = 1; i <= end; i++) {
result.add(i);
}
for (int i = start; i <= n; i++) {
result.add(i);
}
return result;
}
}
C++ 的代码我没有写,这是其他人相同算法的代码。
第二题:你可以获得的最大硬币数目
有 3n 堆数目不一的硬币,你和你的朋友们打算按以下方式分硬币:
- 每一轮中,你将会选出任意
3堆硬币(不一定连续)。 - Alice 将会取走硬币数量最多的那一堆。
- 你将会取走硬币数量第二多的那一堆。
- Bob 将会取走最后一堆。
- 重复这个过程,直到没有更多硬币。
- 给你一个整数数组
piles,其中piles[i]是第i堆中硬币的数目。
返回你可以获得的最大硬币数目。
示例:
输入:piles = [2,4,1,2,7,8]
输出:9
解释:选出 (2, 7, 8) ,Alice 取走 8 枚硬币的那堆,你取走 7 枚硬币的那堆,Bob 取走最后一堆。
选出 (1, 2, 4) , Alice 取走 4 枚硬币的那堆,你取走 2 枚硬币的那堆,Bob 取走最后一堆。
你可以获得的最大硬币数目:7 + 2 = 9.
考虑另外一种情况,如果选出的是 (1, 2, 8) 和 (2, 4, 7) ,你就只能得到 2 + 4 = 6 枚硬币,这不是最优解。
分析
这道题有点贪心算法的影子在里面,为了自己拿数量最大化,所以最好的情况是 Alice 拿最多的,同时 Bob 必须拿最少的,所以就依照这个条件来进行遍历求和即可。
代码
Python
class Solution:
def maxCoins(self, piles: List[int]) -> int:
piles.sort() # 从小到大排序,方便后续处理
left = 0
right = len(piles) - 1
count = 0
while left < right:
if right - 1 >= left: # 如果自己还能够拿一份的话,等于是因为自己比 Bob 先拿
count += piles[right - 1] # 求和
right -= 2 # 我和 Alice 拿完
left += 1 # Bob 拿完
return count
C++
class Solution {
public:
int maxCoins(vector<int>& piles) {
sort(piles.begin(), piles.end(), [](int l, int r) -> bool {
return l > r;
});
int anw = 0;
for(int i = 0; i < piles.size()/3; i++) {
anw += piles[i*2+1];
}
return anw;
}
};
第三题:查找大小为 M 的最新分组
给你一个数组 arr,该数组表示一个从 1 到 n 的数字排列。有一个长度为 n 的二进制字符串,该字符串上的所有位最初都设置为 0 。
在从 1 到 n 的每个步骤 i 中(假设二进制字符串和 arr 都是从 1 开始索引的情况下),二进制字符串上位于位置 arr[i] 的位将会设为 1 。
给你一个整数 m ,请你找出二进制字符串上存在长度为 m 的一组 1 的最后步骤。一组 1 是一个连续的、由 1 组成的子串,且左右两边不再有可以延伸的 1 。
返回存在长度恰好为 m 的一组 1 的最后步骤。如果不存在这样的步骤,请返回 -1 。
示例:
输入:arr = [3,5,1,2,4], m = 1
输出:4
解释:
步骤 1:"00100",由 1 构成的组:["1"]
步骤 2:"00101",由 1 构成的组:["1", "1"]
步骤 3:"10101",由 1 构成的组:["1", "1", "1"]
步骤 4:"11101",由 1 构成的组:["111", "1"]
步骤 5:"11111",由 1 构成的组:["11111"]
存在长度为 1 的一组 1 的最后步骤是步骤 4 。
分析
一开始我直接按着描述,又写了一个典型的超时例子:
class Solution:
def findLatestStep(self, arr: List[int], m: int) -> int:
count = 0
numstr = '0' * len(arr)
for n in range(len(arr)):
numstr = numstr[:arr[n] - 1] + '1' + numstr[arr[n]:]
temp = numstr.split('0')
if '1' * m in temp:
count = n + 1
if count == 0:
return -1
else:
return count
后来找到了另一种解决方法,就是把原来的列表反过来匹配,这样速度会更快;相当于每一次从列表中把一个 1 变为 0,然后每次变换都检查一遍即可。
代码
Python
class Solution:
def findLatestStep(self, arr: List[int], m: int) -> int:
if m == len(arr):
return m
l = [0, len(arr) + 1]
for i, t in enumerate(arr[::-1]):
idx = bisect.bisect(l, t) # 利用 bisect 找到插入位置
l.insert(idx, t)
if l[idx + 1] - l[idx] - 1 == m or l[idx] - l[idx-1] - 1 == m:
# 满足条件即最后一个,可直接返回
return len(arr) - i - 1
return -1
C++
C++ 因为时间问题,就没有写了。
第四题:石子游戏 V
几块石子排成一行,每块石子都有一个关联值,关联值为整数,由数组 stoneValue 给出。
游戏中的每一轮:Alice 会将这行石子分成两个非空行(即,左侧行和右侧行);Bob 负责计算每一行的值,即此行中所有石子的值的总和。Bob 会丢弃值最大的行,Alice 的得分为剩下那行的值(每轮累加)。如果两行的值相等,Bob 让 Alice 决定丢弃哪一行。下一轮从剩下的那一行开始。
只剩下一块石子时,游戏结束。Alice 的分数最初为 0 。
返回Alice 能够获得的最大分数。
示例:
输入:stoneValue = [6,2,3,4,5,5]
输出:18
解释:在第一轮中,Alice 将行划分为 [6,2,3],[4,5,5] 。左行的值是 11 ,右行的值是 14 。Bob 丢弃了右行,Alice 的分数现在是 11 。
在第二轮中,Alice 将行分成 [6],[2,3] 。这一次 Bob 扔掉了左行,Alice 的分数变成了 16(11 + 5)。
最后一轮 Alice 只能将行分成 [2],[3] 。Bob 扔掉右行,Alice 的分数现在是 18(16 + 2)。游戏结束,因为这行只剩下一块石头了。
分析
这一道题没有做出来,自己一开始的想法就想错了(还是太菜了),我用 DFS 发现做不出结果,最后看了大家的代码发现应该使用 DP 去求解(逃)。
代码
Python
import sys
sys.setrecursionlimit(999999999)
class Solution:
def stoneGameV(self, stoneValue: List[int]) -> int:
n = len(stoneValue)
S = [val for val in stoneValue]
for i in range(1, n):
S[i] += S[i - 1]
@lru_cache(typed=False, maxsize=128000000)
def dp(i, j):
if i == j:
return 0
start_val = 0 if i == 0 else S[i - 1]
total = S[j] - start_val
ans = 0
for mid in range(i, j):
part1 = S[mid] - start_val
part2 = total - part1
tmp = None
if part1 < part2:
tmp = part1 + dp(i, mid)
elif part1 > part2:
tmp = part2 + dp(mid + 1, j)
else:
tmp = max( part1 + dp(i, mid), part2 + dp(mid + 1, j) )
ans = max(ans, tmp)
return ans
return dp(0, n - 1)
C++
C++ 因为时间问题,就没有写了。