话不多说,这次直接切入主题,介绍一种牺牲准确性的哈希加速方法——布隆过滤器。这种数据结构及其算法原理较为简单,所以内容不会过于复杂。
什么是布隆过滤器(Bloom Filter)
布隆过滤器(英语:Bloom Filter)是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率和删除困难。
上面是来自维基百科的介绍,详情可见布隆过滤器 - 维基百科。
说白了,布隆过滤器就类似与 set() 的操作,可以用于匹配特定键是否在集合之中。其原理也很简单,就是使用了多个哈希函数对键进行哈希得出多个值,然后将内存中对应位置设置为 1,如下图所示(来源见水印):
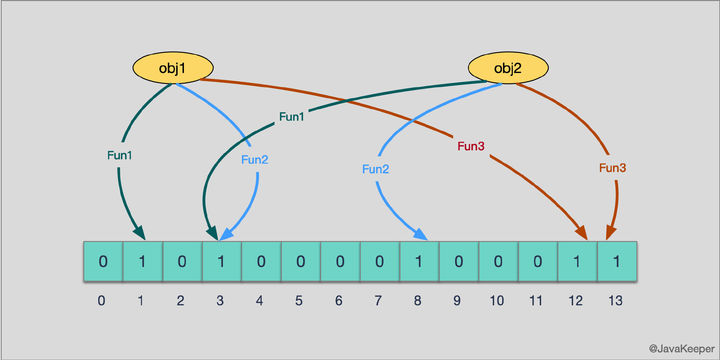
当我们有一个 obj1 和 obj2 时,首先用 3 个 Hash 函数进行哈希得出对应的地址,然后依次设为 1,即可实现写入布隆过滤器的过程。
归纳一下具体的算法步骤:
- 初始化 k 个 Hash 函数,同时保证其能够分别哈希到不同的内存位置;
- 初始化一个长度为 n 比特的数组(bitarray/bitmap),每个位都设置为
0; - 加入 key 时,先散列出 k 个地址,并将该位置的数据设置为
1; - 查找 key 时,同样散列出 k 个地址,然后查询内存对应的内存位置,若全为
1可认为在集合中,若有0则一定不在集合中。
该算法的缺点十分明显,因为位置存在重复性,所以不能够进行删除操作;同时,由于查询出来的内存位置此时可能已经有了其他的键 Hash 出来的 1,所以全为 1 的时候存在一定的误判率——当然,有 0 就已经可以证明该键并没有经过哈希了,不会发生误判。
这时候相信很多人会有一个疑问:为什么不用直接用哈希表呢?正常情况下,为了保证哈希表 $O(1)$ 的复杂度以及防止哈希冲突,哈希表的存储效率通常在 50% 以下,这就意味着哈希表往往都会较大,而布隆过滤器不用存键值,而且更加“紧凑”,所以可以在相对于小的内存里提供较好的查找性能。但代价就是存在一定的误判率,业务中也需要进行该方面的考量。
当数据量较小的时候,直接使用哈希表便可以优雅地解决问题了;此时使用布隆过滤器反而还需要承担额外不必要的错误率,得不偿失。
常用场景
实际的应用场景中,布隆过滤器广泛地应用于网页黑名单系统、垃圾邮件过滤系统、网页 URL 去重、垃圾邮件识别、大集合中重复元素的判断和缓存穿透等。下面是一些详细的场景:
- 数据库防止穿库。 Google Bigtable,HBase 和 Cassandra 以及 Postgresql 使用BloomFilter来减少不存在的行或列的磁盘查找。避免代价高昂的磁盘查找会大大提高数据库查询操作的性能。
- 业务场景中判断用户是否阅读过某视频或文章,比如抖音或头条,当然会导致一定的误判,但不会让用户看到重复的内容。
- 缓存宕机、缓存击穿场景,一般判断用户是否在缓存中,如果在则直接返回结果,不在则查询db,如果来一波冷数据,会导致缓存大量击穿,造成雪崩效应,这时候可以用布隆过滤器当缓存的索引,只有在布隆过滤器中,才去查询缓存,如果没查询到,则穿透到db。如果不在布隆器中,则直接返回。
- WEB拦截器,如果相同请求则拦截,防止重复被攻击。用户第一次请求,将请求参数放入布隆过滤器中,当第二次请求时,先判断请求参数是否被布隆过滤器命中。可以提高缓存命中率。Squid 网页代理缓存服务器在 cache digests 中就使用了布隆过滤器。Google Chrome浏览器使用了布隆过滤器加速安全浏览服务
- Venti 文档存储系统也采用布隆过滤器来检测先前存储的数据。
- SPIN 模型检测器也使用布隆过滤器在大规模验证问题时跟踪可达状态空间。
(摘自愚公要移山的答案)
相关参数的计算
假设输入对象个数为 $n$,bitarray 的大小为 $m$,所容忍的误判率 $p$ 和哈希函数的个数 $k$。则有:
$$ m=\frac{n\times\ln p}{(\ln2)^2} $$
$$ k=\ln2\times\frac{m}{n}=0.7\times\frac{m}{n} $$
$$ p = (1-e^{-\frac{nk}{m}})^k $$
其中的 $m$ 和 $k$ 因为在一定范围内是越高越好,所以小鼠部分需要进行向上取整。
尾巴
总的来说,布隆过滤器是一个十分简单而有效的、基于哈希算法的优化算法。它能够在限制相对较高的空间中提供一个较好的查找功能,但是会具有一定的误判率。误判率一般情况下很小,且会随着 bitarray 使用率的升高而增大。因此,该算法更适合于判重、查重之类只需要判断不存在特定键的场景;对于查找特定键是否存在的场景就需要针对其特性做出综合考量。